Dynamic programming là gì? Tại sao bạn nên quan tâm
Dynamic programming là phương pháp phân chia vấn đề lớn thành những vấn đề nhỏ hơn để giải quyết hiệu quả hơn. Khám phá thuật ngữ "memoization" và mối liên hệ của nó với Dynamic programming trong bài viết dưới đây.
Tại Sao Bạn Nên Quan Tâm?
Dynamic programming là quá trình phân chia một vấn đề lớn thành nhiều vấn đề nhỏ hơn. Bằng cách sử dụng các giải pháp của những vấn đề nhỏ hơn này, chúng ta có thể tìm ra giải pháp tổng thể một cách hiệu quả hơn.
Chúng ta cũng sẽ tìm hiểu về thuật ngữ "memoization" và mối liên hệ của nó với Dynamic programming .
Làm Thế Nào Nó Hoạt Động?
Ví dụ thường thấy của Dynamic programming là Dãy số Fibonacci. Đó là một ví dụ hay, vì vậy chúng ta sẽ sử dụng nó ở đây. Nếu bạn đã quen thuộc với Dãy số Fibonacci (và cách tính nó bằng đệ quy), thì bạn có thể bỏ qua phần tiếp theo.
Nếu bạn không chắc chắn điều đó có nghĩa là gì, hoặc bạn muốn ôn lại nhanh, hãy đọc tiếp...
Dãy Số Fibonacci
Đây là một chuỗi các số, trong đó mỗi số được tính bằng cách cộng hai số trước đó với nhau:
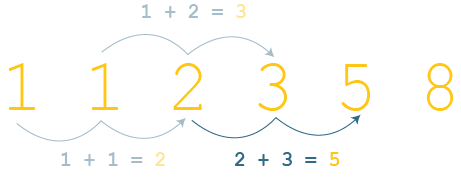
Dãy Số Fibonacci
Hãy tưởng tượng tôi yêu cầu bạn tính toán số thứ sáu trong dãy (là 8, như đã hiển thị ở trên).
Bạn sẽ tính nó như thế nào?
Dưới đây là đoạn mã JavaScript cho một hàm có chức năng đó:
function f(n) // Giá trị đầu tiên và thứ hai luôn là 1 if (n == 1 || n == 2) return 1; // Tính toán hai giá trị trước đó trong dãy số // sử dụng cùng một hàm này return f(n - 1) + f(n - 2) // Tính toán giá trị thứ sáu trong dãy số let answer = f(6) Phương pháp này sẽ hoạt động tốt, nhưng nó chậm.
Bạn có thể thấy rằng hàm gọi chính nó; nó là đệ quy.
Để tính số Fibonacci thứ sáu, chúng ta trước tiên cần tính số thứ tư và thứ năm.
Mỗi số trong những số đó lại tiếp tục tính số trước của chúng, và điều này lặp lại cho đến khi trở về đầu chuỗi.
Dưới đây là hình ảnh của nó nếu chúng ta vẽ nó ra dưới dạng một đồ thị.
Bạn có thể thấy rằng có rất nhiều sự trùng lặp ở đây. Ví dụ, giá trị thứ hai trong dãy được tính tới năm lần!
Đối với những số nhỏ trong dãy, điều này không quá tệ, nhưng càng về sau càng tệ hơn. Đối với những số sau này trong dãy, việc tính toán sẽ trở nên không thực tế, thậm chí trên một máy tính hiện đại.
Dynamic programming và Memoization
Một cách chúng ta có thể cải thiện hàm này là lưu trữ kết quả của các phép tính trước đó khi chúng ta tiếp tục tiến hành. Như vậy, chúng ta chỉ cần tính toán mỗi số trong dãy số Fibonacci một lần.
Đây chính là bản chất của Dynamic programming :
Dynamic programming là việc phân chia vấn đề lớn thành các vấn đề nhỏ hơn, và sử dụng chúng để đạt được câu trả lời.
Vì chúng ta đạt được điều này bằng cách lưu trữ kết quả trước đó để sử dụng sau, chúng ta cũng đang sử dụng memoization:
Memoization là việc lưu trữ kết quả của một phép tính trước đó để chúng ta có thể sử dụng sau, làm cho thuật toán tổng thể hiệu quả hơn.
Chúng ta có thể áp dụng những khái niệm này vào cách tiếp cận đệ quy ở trên, nhưng sẽ dễ theo dõi hơn nếu chúng ta sử dụng cách tiếp cận "từ dưới lên".
Hãy xem xét đoạn mã trước, và sau đó chúng ta có thể thảo luận tại sao đây được gọi là thuật toán từ dưới lên:
function f(n) // Giá trị đầu tiên và thứ hai luôn là 1 if (n == 1 || n == 2) return 1 let result = 0 // Dùng để lưu trữ hai kết quả trước đó let lastButOneValue = 1 let lastValue = 1 // Bắt đầu từ phần tử thứ 3 của dãy số (các phần tử 1 và 2 là // trường hợp đặc biệt, xem ở trên), tính toán từng giá trị lần lượt for (let i = 3; i <= n; i++) // Tính số này bằng cách cộng hai số trước đó lại với nhau result = lastValue + lastButOneValue // Cập nhật giá trị của hai phần tử // trước đó trong dãy số lastButOneValue = lastValue lastValue = result return result // Tính toán giá trị thứ sáu trong dãy số let answer = f(6) Ở đây, chúng ta tính toán dãy số Fibonacci theo thứ tự — từ đầu cho đến khi chúng ta đạt được số mà chúng ta cần.
Khi tiến hành, chúng ta lưu trữ kết quả của giá trị trước đó, và giá trị trước đó nữa.
Việc lấy giá trị tiếp theo từ đó trở nên rất đơn giản. Chỉ cần cộng hai giá trị đó lại với nhau.
Dưới đây là đồ thị từ thuật toán ban đầu (không hiệu quả) một lần nữa, nhưng chúng ta chỉ làm nổi bật những phép tính chúng ta thực hiện trong phiên bản mới này:
Bạn có thể thấy rằng lần này, thay vì bắt đầu từ câu trả lời và làm việc ngược lại, chúng ta làm việc tiến lên cho đến khi chúng ta đạt được giá trị cần thiết.
Khi chúng ta hình dung nó, chúng ta đang làm việc từ phần dưới của đồ thị lên trên — do đó là cách tiếp cận "từ dưới lên".
Thuật toán này hiệu quả hơn rất nhiều. Không có sự trùng lặp nào cả!
Tóm Lược
Thuật toán mới nhất của chúng ta sử dụng Dynamic programming , bởi vì chúng ta đang phân chia vấn đề lớn thành các vấn đề nhỏ hơn và sử dụng kết quả của chúng để đạt được câu trả lời tổng thể.
Nó cũng sử dụng memoization, vì chúng ta lưu trữ kết quả của bước trước để tránh phải tính toán lại sau này.
Đó là một cách tiếp cận từ dưới lên, bởi vì khi chúng ta hình dung vấn đề dưới dạng đồ thị, chúng ta đang làm việc từ đáy của đồ thị lên trên** (không giống như thuật toán kém hiệu quả, mà là từ trên xuống).