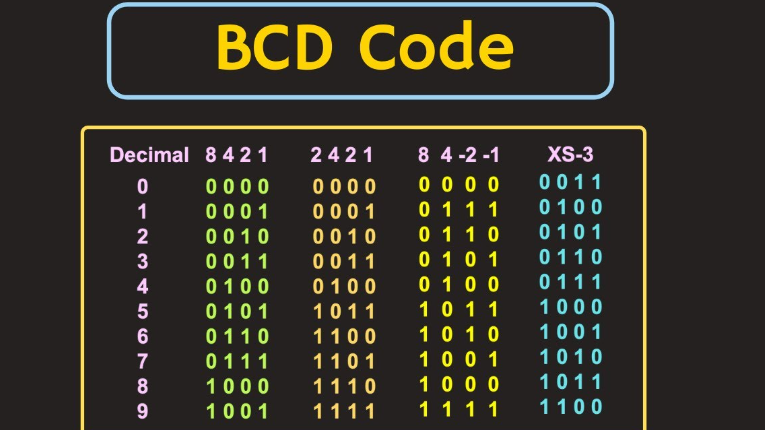
BCD là gì? Ưu nhược điểm của mã hóa nhị phân số thập phân
Trong các mạch điện tử và kỹ thuật số, mã hóa nhị phân số thập phân BCD thường được sử dụng rộng rãi, mỗi mã lại có cách sử dụng riêng. Vậy BCD là gì và các ưu điểm, nhược điểm của mã hóa này được thể hiện như thế nào? Hãy cùng Bizfly Cloud tìm hiểu ở bài viết dưới đây!
BCD là gì?
BCD là một loại biểu diễn nhị phân cho các giá trị thập phân, trong đó mỗi chữ số được biểu diễn bằng một số cố định các bit nhị phân, thường là từ bốn đến tám bit. Nhưng thông thường là bốn bit, biểu diễn hiệu quả các giá trị thập phân từ 0 đến 9.

BCD là gì?
Hệ thống định dạng viết này được sử dụng vì không có giới hạn về kích thước của một số. Bốn bit có thể được thêm vào như một chữ số thập phân khác, so với biểu diễn nhị phân thực, bị giới hạn ở các lũy thừa thông thường của hai, chẳng hạn như 16, 32 hoặc 64 bit.
Bảng chuyển đổi số thập phân sang nhị phân
Dưới đây là bảng chuyển đổi các số từ 0 đến 15 từ hệ thập phân (decimal) sang hệ nhị phân (binary):
Decimal (Thập phân) | Binary (Nhị phân) |
0 | 0000 |
1 | 0001 |
2 | 0010 |
3 | 0011 |
4 | 0100 |
5 | 0101 |
6 | 0110 |
7 | 0111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
11 | 1011 |
12 | 1100 |
13 | 1101 |
14 | 1110 |
15 | 1111 |
Bảng này có thể được mở rộng để bao gồm các số lớn hơn. Để chuyển đổi một số từ hệ thập phân sang hệ nhị phân, ta có thể dùng phương pháp chia liên tiếp cho 2, ghi lại phần dư và đọc ngược lại các phần dư để có kết quả cuối cùng.
Một số ví dụ về chuyển đổi thập phân sang nhị phân và ngược lại
Ví dụ 1: Số thập phân = 1764
Biểu diễn thập phân được mã hóa nhị phân được biểu diễn như sau:
1 | 7 | 6 | 4 |
0001 | 0111 | 0110 | 0100 |
Ví dụ 2
Số thập phân = 238
Biểu diễn thập phân được mã hóa nhị phân được biểu diễn như sau:
2 | 3 | số 8 |
0010 | 0010 | 0010 |
Ví dụ 3
Số thập phân = 1895
Biểu diễn thập phân được mã hóa nhị phân được biểu diễn như sau:
1 | số 8 | 9 | 5 |
0001 | 1000 | 1001 | 0101 |
Biểu diễn thập phân được mã hóa nhị phân của một số không giống với biểu diễn nhị phân đơn giản của nó. Ví dụ: ở dạng nhị phân, số thập phân 1895 xuất hiện dưới dạng 11101100111. Ở dạng thập phân mã hóa nhị phân, nó xuất hiện dưới dạng 0001100010010101.
Ưu, nhược điểm của BCD so với các loại mã hóa khác
1. Về ưu điểm
Quá trình chuyển đổi được đơn giản hóa: BCD giúp việc chuyển đổi giữa số nhị phân và thập phân trở nên dễ dàng hơn, đặc biệt hữu ích trong các ứng dụng máy tính và thiết bị kỹ thuật số liên quan đến xử lý số liệu thập phân như máy tính bỏ túi, đồng hồ số và các hệ thống tài chính.
Giảm sai số trong tính toán thập phân: Vì BCD biểu diễn chính xác từng chữ số thập phân, nó giúp tránh được các sai số chuyển đổi có thể xảy ra khi sử dụng hệ thống nhị phân truyền thống, đặc biệt khi làm việc với số liệu tài chính.
Dễ hiểu và dễ sửa lỗi: Do mỗi chữ số thập phân được mã hóa độc lập, việc xác định và sửa lỗi (nếu có) dễ dàng hơn. Ví dụ, nếu một nhóm bốn bit bị lỗi, chỉ cần sửa lại nhóm đó mà không ảnh hưởng đến toàn bộ số.
2. Về nhược điểm
Hiệu quả bộ nhớ thấp: BCD sử dụng 4 bit để biểu diễn một chữ số thập phân (0-9). Do đó, không gian bộ nhớ không được sử dụng tối ưu vì chỉ 10 trong số 16 giá trị có thể (0000 đến 1111) thực sự được sử dụng.
Hiệu suất tính toán thấp hơn: Các phép toán trên BCD phức tạp hơn so với các phép toán trên số nhị phân thuần túy, vì phải xử lý từng chữ số thập phân riêng lẻ và có thể cần phải điều chỉnh kết quả để đảm bảo tính hợp lệ của BCD.
Không thích hợp cho các ứng dụng khoa học và kỹ thuật: Trong các ứng dụng khoa học và kỹ thuật, các giá trị số thường rất lớn hoặc rất nhỏ, và thường cần tính toán phức tạp. BCD không phù hợp cho các trường hợp này vì không gian bộ nhớ lớn và hiệu suất tính toán kém.
Mục đích chính khi sử dụng mã BCD so với mã nhị phân thông thường
So với mã nhị phân thông thường, việc sử dụng mã BCD thường phù hợp với các mục đích sau đây:

Mục đích chính khi sử dụng mã BCD
Dễ chuyển đổi: Mã BCD thể hiện mỗi chữ số thập phân bằng bốn bit nhị phân, làm cho việc chuyển đổi giữa số thập phân và số nhị phân trở nên đơn giản hơn. Điều này hữu ích trong các ứng dụng yêu cầu hiển thị số liệu cho người dùng.
Giảm thiểu lỗi khi chuyển đổi: Khi làm việc với số liệu thập phân trong các hệ thống kỹ thuật số, việc chuyển đổi qua lại giữa thập phân và nhị phân có thể gây ra lỗi. Mã BCD giúp giảm thiểu các lỗi này bằng cách duy trì cấu trúc số thập phân.
Tối ưu hóa trong các ứng dụng tài chính và kế toán: Trong các ứng dụng tài chính, kế toán và thương mại điện tử, số liệu thường được xử lý và lưu trữ ở dạng thập phân. Sử dụng mã BCD giúp dễ dàng hơn trong việc tính toán và hiển thị các con số này một cách chính xác.
Dễ dàng xử lý các phép toán thập phân: Một số vi điều khiển và hệ thống nhúng hỗ trợ các phép toán trên số BCD trực tiếp, giúp tăng hiệu quả trong việc xử lý các số liệu thập phân mà không cần phải chuyển đổi sang nhị phân và ngược lại.
Tránh được một số lỗi số học trong tính toán nhị phân: Một số phép tính nhị phân có thể dẫn đến các lỗi làm tròn và chính xác do giới hạn của kiểu dữ liệu nhị phân. Mã BCD giúp tránh được các lỗi này bằng cách duy trì số liệu ở dạng thập phân suốt quá trình tính toán.
So sánh BCD với một số mã chuyển đổi khác
Loại mã chuyển đổi | Đặc điểm | Ưu điểm | Nhược điểm |
BCD | Mỗi chữ số thập phân (0-9) được biểu diễn bằng 4 bit | · Dễ dàng chuyển đổi giữa biểu diễn thập phân và nhị phân. · Phù hợp cho các ứng dụng tài chính và thương mại nơi cần xử lý số thập phân. | · Hiệu quả lưu trữ không cao do sử dụng 4 bit cho mỗi chữ số, dẫn đến lãng phí không gian khi so với biểu diễn nhị phân trực tiếp. · Các phép toán số học phức tạp hơn. |
ASCII | Mỗi ký tự (chữ cái, số, ký hiệu, ký tự điều khiển) được mã hóa bằng một chuỗi 7 hoặc 8 bit. | · Chuẩn quốc tế, sử dụng rộng rãi cho văn bản và truyền thông máy tính. Đầy đủ các ký tự in được và ký tự điều khiển. | Không thích hợp cho các phép toán số học trực tiếp vì cần phải chuyển đổi giữa ký tự và giá trị số. |
EBCDIC | Mỗi ký tự được mã hóa bằng 8 bit. | · Sử dụng chủ yếu trong hệ thống mainframe của IBM. · Hỗ trợ đầy đủ ký tự chữ cái, số và ký tự điều khiển. | Ít phổ biến hơn ASCII, chủ yếu giới hạn trong các hệ thống IBM.
|
Gray Code | Mã nhị phân không trọng số, trong đó hai giá trị liên tiếp chỉ khác nhau một bit | Giảm thiểu lỗi trong các hệ thống điện tử, đặc biệt trong việc đọc các giá trị từ các thiết bị quay số. | Không trực tiếp sử dụng trong các phép toán số học |
Excess-3 | Mỗi chữ số thập phân được mã hóa bằng 4 bit với giá trị là số BCD cộng thêm 3. | · Tránh các mã không hợp lệ của BCD (như 1010 đến 1111). · Hỗ trợ phát hiện lỗi. | · Phức tạp hơn BCD trong việc mã hóa và giải mã. · Hiệu quả lưu trữ không cao do sử dụng 4 bit cho mỗi chữ số. |
Mã nhị phân | Mỗi số được biểu diễn trực tiếp bằng chuỗi bit nhị phân | · Hiệu quả lưu trữ cao. · Dễ dàng thực hiện các phép toán số học. | · Chuyển đổi giữa nhị phân và thập phân phức tạp hơn. · Không tự nhiên để làm việc với các số thập phân, đặc biệt trong các ứng dụng tài chính và thương mại. |
Trên đây, Bizfly Cloud vừa cung cấp đến bạn những thông tin liên quan đến BCD là gì, các ưu điểm và nhược điểm của mã hóa nhị phân số thập phân này. Chúng tôi hy vọng đã mang đến cho bạn thông tin hữu ích để sử dụng và áp dụng BCD hiệu quả.