Giới thiệu thuật toán greedy
I, Giới thiệu thuật toán greedy
Trong bài viết này, mình sẽ giới thiệu về một loại thuật toán khá thú vị là greedy algorithm (thuật toán tham lam). Hướng giải quyết của loại thuật toán này là luôn chọn phương án tốt nhất ở thời điểm hiện tại. Việc tối ưu cục bộ (locally optimal) này với hy vọng rằng kết quả trên toàn cục sẽ được tối ưu (globally-optimal solution).
II, Ưu nhược điểm
Thuật toán greedy có vài ưu và nhước điểm như sau:
Ưu điểm:
Dễ dàng đưa ra cách giải quyết với hướng thuật toán greedy Dễ dàng phân tích space và time complexity so với các techniques khác (như Divide and Conquer approach)
Nhược điểm:
Chứng minh tính đúng đắn của một thuật toán khó hơn các techniques khác
Bài toán ví dụ 1 - Tandem Bicycle
Đề bài: xe đạp đôi được di chuyển bởi 2 riders mặc áo đỏ và xanh. Cả hai người đều đạp nhưng tốc độ của xe bằng tốc độ của người đạp nhanh hơn. Đầu vào là hai list chứa tốc độ của riders mặc áo đỏ và xanh. Trả về tổng tốc độ cao nhất của các cặp bikers.
Input:
red_shirts = [5, 5, 3, 9, 2]
blue_shirts = [3, 6, 7, 2, 1] Output:
32 # 7 + 6 + 5 + 5 + 9 Cách giải quyết:
Thời Chiến Quốc, Tôn Tẫn - cháu của Tôn Tử (tác giả quyển Binh pháp Tôn Tử) là quân sư lỗi lạc của nước Tề. Trong cuộc đua ngựa của Điền Kỵ với vua Uy Vương, Tôn Tẫn đã hiến diệu kế cho Điền Kỵ như sau:
Ngựa được chia thành ba loại: hạ, trung, thượng. Dùng ngựa "hạ đẳng" của mình để đấu với ngựa "thượng đẳng". Dùng ngựa "trung đẳng" của mình đấu với ngựa "hạ đẳng". Và lấy ngựa "thượng đẳng" của mình đấu với ngựa "trung đẳng". Như vậy sẽ thua 1 thắng 2; từ đó giành chiến thắng chung cuộc
Cách giải quyết bài này cũng tương tự như cách trên: Chúng ta ghép những người chạy nhanh nhất (ngựa thượng đẳng) ở một team ghép với những người chạy chậm nhất (ngựa hạ đẳng) ở team còn lại. Vì tốc độ của xe bằng tốc độ của người đạp nhanh nhất, do đó tổng tốc độ của các cặp sẽ là lớn nhất. Cách chi tiết như sau:
- Sort một list; sort list còn lại theo hướng ngược lại.
- Zip sorted list tạo thành các cặp gồm một thành viên áo xanh và một thành viên áo đỏ.
- Tính speed của các xe của cặp bằng công thức max(red_speed, blue_speed).
- Tính tổng speed của các cặp
Lời giải bằng Python của mình:
def tandemBicycle(redShirtSpeeds, blueShirtSpeeds, fastest):
redShirtSpeeds.sort()
blueShirtSpeeds.sort(reverse=fastest)
rs_speed = 0
for red, blue in zip(redShirtSpeeds, blueShirtSpeeds):
speed = max(red, blue)
rs_speed += speed
return rs_speed
Phân tích space và time complexity
Chú thích: n là số lượng phần tử đầu vào
Space complexity là O(1)
- Vì toàn bộ thuật toán xử lý ngay trên chính hai list đầu vào nên space complexity là constant - O(1)
Time complexity là O(nlogn)
- Time complexity để sort 2 list là O(nlogn) Time complexity để tính speed của các pairs sẽ là O(n) Do đó tổng time complexity là O(nlogn)
Lưu ý: hệ số log trong Computer Science mặc định là 2 chứ không phải là 10.
Bài toán ví dụ 2 - Minimum Waiting Time
Đề bài: Nhận một list gồm các số nguyên dương thể hiện thời gian cần để thực hiện công việc. Chỉ có một công việc có thể làm trong một thời điểm. Thời gian chờ là thời gian cần chờ trước khi thực hiện công việc tiếp theo. Ví dụ nếu công việc được thực hiện thứ hai thì thời gian chờ là thời gian cần để thực hiện công việc đầu tiên. Viết một function trả về số lượng thời gian chờ thấp nhận cho toàn bộ công việc đầu vào.
Input:
[5, 1, 7, 8] Output:
24 # 0 + 5 + (5 + 1) + (5 + 1 + 7) Cách giải quyết:
Để tối ưu thời gian chờ thấp nhất, chúng ta sẽ tận dụng thời gian của công việc càng về cuối càng ít ảnh hưởng đến . Do đó, chúng ta sẽ xếp những công việc có thời gian thực hiện lâu ở cuối. Mô tả cách giải như sau:
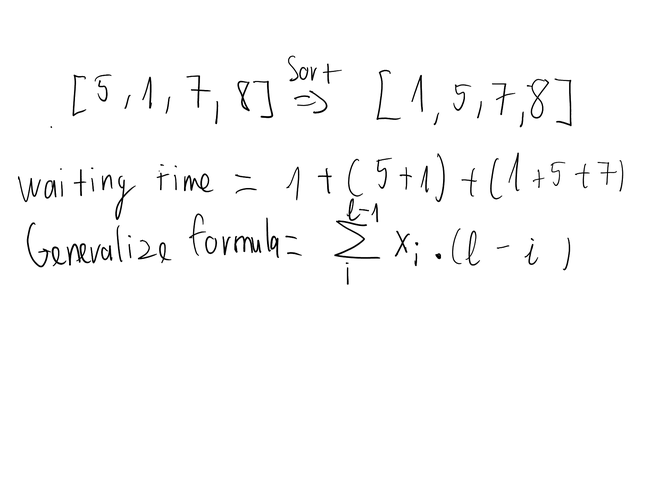
algorithm illustration
Cách giải chi tiết:
- Đầu tiên chúng ta sort input list
- Ta có thể nhận ra ví dụ waiting time ở trên là thời gian thực hiện một task nào đấy xuất hiện ở thời gian chờ ở các task sau. Nghĩa là tổng thời gian chờ sẽ gồm (length - i) * n (với length là độ dài của list, i là index hiện tại và n là thời gian thực hiện task hiên tại)
- Do đó chúng ta sẽ sử dụng công thức generalized formula ở trên để tính ra thời gian chờ ít nhất
Lời giải như sau:
def minimumWaitingTime(queries):
queries.sort()
minimum_waiting_time = 0
for i, query in enumerate(queries[:-1], start=1):
minimum_waiting_time += query * (len(queries) - i)
return minimum_waiting_time Phân tích space và time complexity:
Space complexity là O(1)
Vì chúng ta xử lý trên chính input list nên space complexity là constant - O(1)
Time complexity là O(nlogn)
- Time complexity để sort list là O(nlogn)
- Time complexity để lặp qua list nhằm tính waiting time là O(n)
- Do đó tổng complexity là O(nlogn)
Kết luận
Mong rằng bài viết đã cung cấp cho các bạn cái nhìn tổng quan về greedy algorithm. Nếu bạn thấy bài blog thú vị hãy chia sẻ để nhiều người biết đến hơn nhé Và hãy đón chờ thêm các bài blog của mình về chủ đề Data Structure & Algorithm trên tech blog của Bizfly Cloud nha!